关键词： 条件概率(conditional probabilities), 贝叶斯规则(Baye's rules)，全概率(Total probability Theorem)

参考资料： MOOC学堂在线-概率论， 阮一峰的日志《贝叶斯推断及其互联网应用（一）：定理简介》

 

前几个周把抱着浏览的心态在P5的前三个算法给看了一遍，但没有理解多少，今天拿着《机器学习》的书，认真的进行了学习，发现贝叶斯统计其实很好理解。简单做一个整理。

先从一个让我产生顿悟的例子讲起，来自概率论课程中

A radar example- 雷达问题

 

先从一个最经典的例子入手（我第一次看的时候完全没搞懂，今天重新讲讲）——假阳性问题

 

 

 

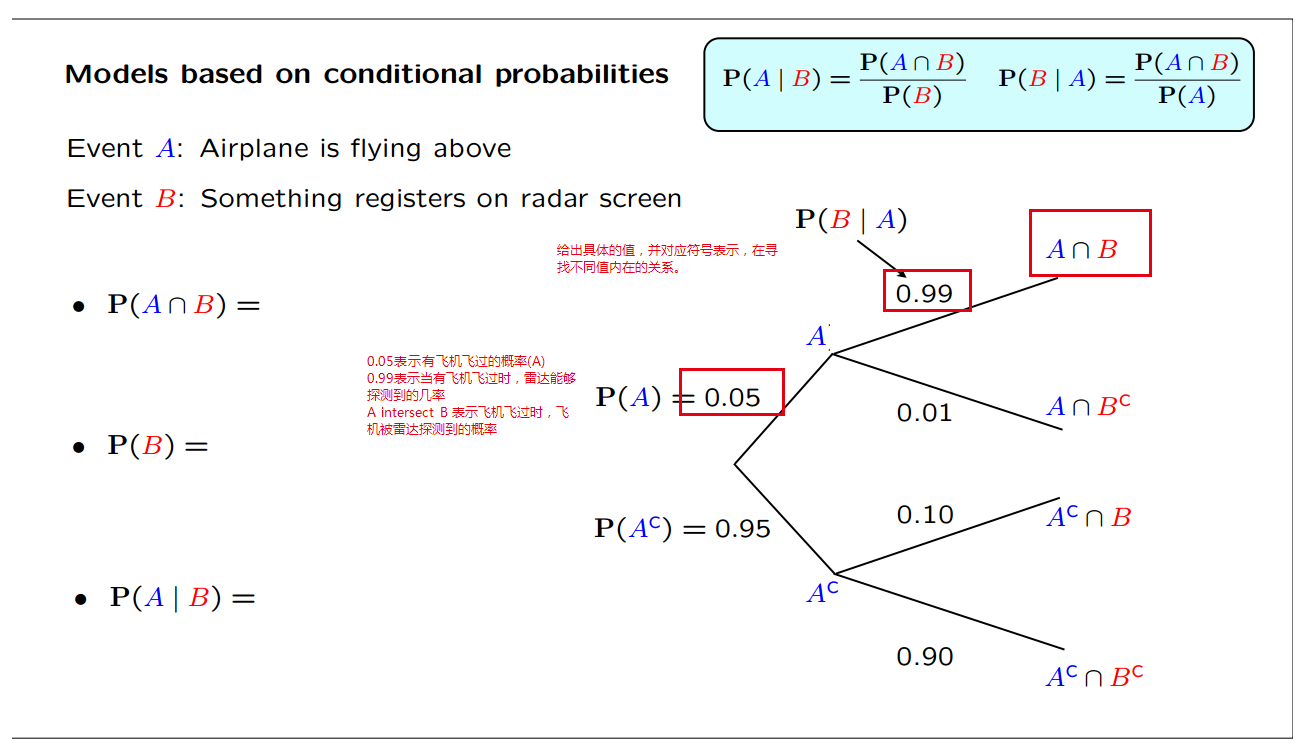
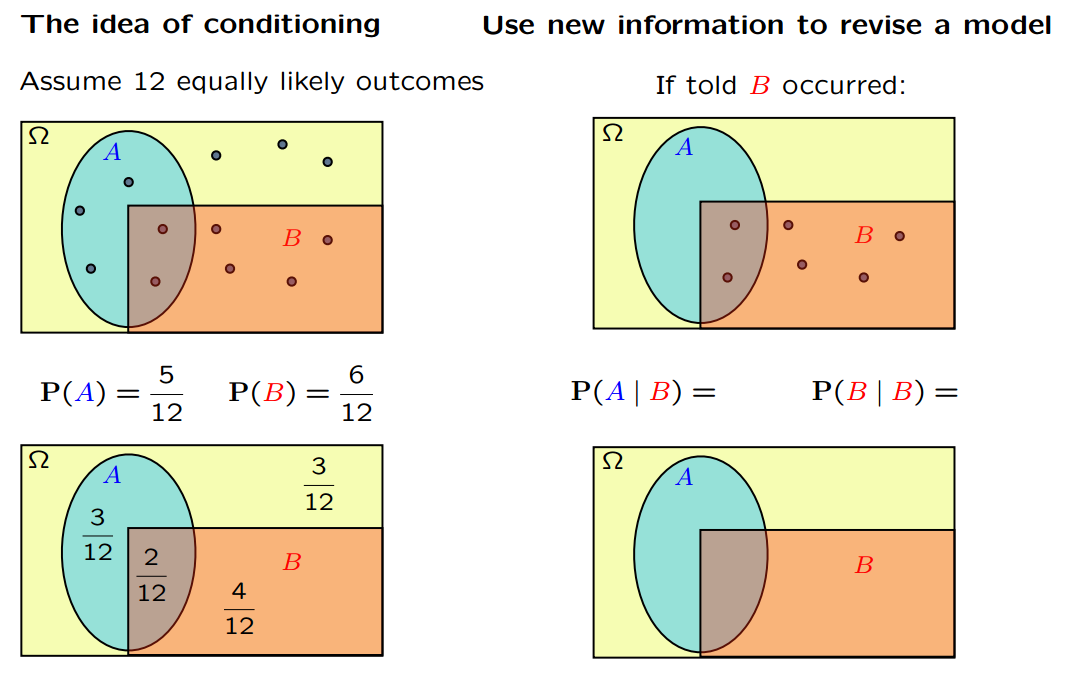
条件概率不是theorem 而只是一个definintion，是不同概率值的相互比率关系，目的在于根据新的信息作出再判断。当看到树形结构图时，便联想到了决策树模型，当你对一个属性进行判断之后，你

就默认该属性是存在的（或者说是已经成立的），在这个判断的基础上，你会再深入到其下的子节点进行下一步的计算和判断，而条件概率就是为了判断这进一步的推断。

计算公式：